Kadane’s algorithm could be a good solution to find maximum subarray in the given list. First let’s describe the maximum subarray problem.

What is the maximum subarray problem

Given an array, find the contiguous subarray with the largest sum.

For instance for this array:

int[] arr = {1, -3, 2, 1, -1};

// Solution is:
int[] result = {2, 1};
// Because [2,1] = 2+1=3 is the max sum

Now let’s clarify the what do we mean by subarray

What is the subarray?

Subarray is a slice of contiguous array that maintains the order of the elements. You would understand better with the example:

For the given array: {1, -3, 2, 1, -1}

• {1} is a subarray (one element could be subarray also)

• {1, -3} is a subarray

• {1, -3, 2} is a subarray

• {1, -3, -1}is not a subarray (because it is not contiguous)

First brute force solution

We may use the brute force with two for loops. But it will take $O(n²)$ times which is not efficient

For instance, outer loop starts with index 0, then inner loop starts with index 1:

Kadane’s Algorithm

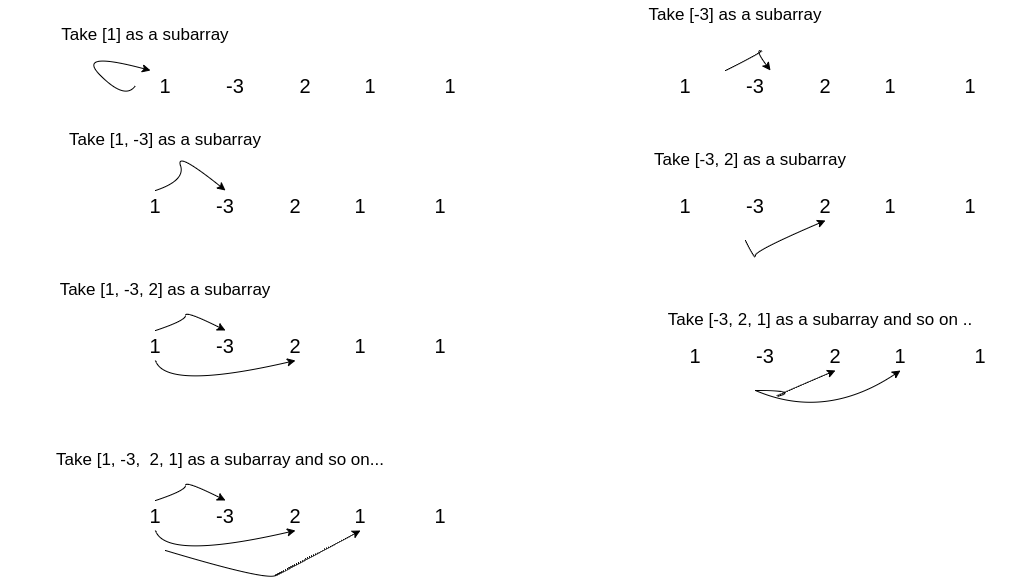
Instead of brute force solution we are going to find an answer what is the maximum subarray at ending index i ?

Here is the picture for the algorithm

Even idea is simple, it will take: $$ O(n²) $$

However, this algorithm can be enhanced and after that it takes only $$O(n)$$

Enhanced Kadane’s Algorithm

Idea is to find local maximum subarray

At index i, local maximum subarray could be:

• just current index itself [i]

• or current element combined with the previous maximum subarray

For instance at index 2:

int[] arr = {1, -3, 2, 1, 1}; // index 2 = arr[2] = 2

At index 2, we can say that :

• Maximum subarray can only contain subarray [2] whose sum is equal to 2

• Or it can be combination of the maximum subarray at index 1 plus maximum subarray which only contains index 2 => [1, -3, 2]

• After we check the both options we can update the maximum global subarray

We won’t apply this strategy for the first element, because it is unnecessary

Here is the pseudocode:

public static int kadane(int[] arr) {
    max_local = max_global = arr[0];
    for i from 1 to (size() - 1) {
        max_local = max(arr[i], max_local + arr[i])

        if (max_local > max_global) {
            max_global = max_local;
        }
    }

    return max_global;
}

Java Implementation

import java.util.*;

public class KadaneAlgorithm {
    public static int kadane(int[] arr) {
        int max_local = arr[0];
        int max_global = arr[0];

        for (int i = 1; i < arr.length; i++) {
            int maximumSubArrayAtIndex_i = arr[i];
            int previousMaximumSubArray = max_local;

            max_local = Math.max(maximumSubArrayAtIndex_i, previousMaximumSubArray + arr[i]);
            if (max_local > max_global) {
                max_global = max_local;
            }
        }
        return max_global;
    }
}