Capture long running method execution in Spring Boot using annotation
It is crucial to capture long running method execution in your application (whether it is an API or traditional mvc application). You should also …
In this article, we are going to dive into the what is the optimal stopping and we are going to write practical implementation with Java.
First, let’s understand what optimal stopping is
What is the optimal stopping? (%37 rule)
In a sentence, optimal stopping means that “how long we should keep looking for something to find the best one”
This can be more understandable with the famous Secretary Problem
Secretary Problem
Problem is so simple:
-
As a CEO,CTO etc.. of a company, you have to find secretary which manages your daily routine.
-
You interview the applicants in random order, one at a time.
-
But you have some restrictions:
-
If you can decide to offer the job to an applicant:
-
There is guarantee that applicant will accept the offer.
-
After any applicant accepts the offer, you are not allowed to interview remaining applicants(you will remove job listing from the platform such as Linkedin)
-
-
Else (means if you pass that applicant),
- There is no chance to offer that applicant again, that applicant will be gone forever
-
Then question is that, how can you increase the chance to find best secretary among the applicant pool?
In this problem, there are two ways we can fail:
-
Stopping early: For example, if we choose the first(or second or third) applicant as the best one, we leave the better ones as undiscovered. (Maybe the fifth one is best among the others??)
-
Stopping late: For example, if we choose the last applicant as the best one, then we can have chance to pass best applicant. Let’s say there are 10 applicants, after interviewing with the fifth applicant ()we know that best applicant is the fifth one), we decided to continue the interview process. While we interviewing the last applicant(10th), we will be able to know that 10th applicant is not better than applicant(5th). Therefore we will miss the choose the best applicant(5th)
The optimal strategy will allow us to find the right balance between stopping early and stopping late
Best rate chance also will decrease over the interview process
We can’t know the next applicant is the best or not until we meet him/her.
If we are interviewing with the first applicant, it is the best one for 100%. Because we don’t know the second applicant.
If we are interviewing with the second applicant, it can be the best one with 50% chance. Because we only knows two applicants, one can be better than other.
If we are interviewing with the third applicant, it can be the best one with 33% chance
…
If we are interviewing with the 100th applicant, it can be the best one with 1% chance
As we can see that chance to finding the best secretary will also descrease over the interview process. Then question will be: “What strategy should we follow to find the best one?”
Optimal solution suggests us the rule called Look-Then-Leap Rule
What is the Look-Then-Leap Rule?
With this rule:
-
We are going to set a predetermined a amount of time for looking
-
In that timeframe, we are going to gather data.
-
Also in that timeframe, we will never choose anyone(any secretary), no matter how they are impressive
-
-
After the looking step, we will enter the leap step:
- At the leap step, we instantly choose the first best applicant which is the better than we saw in the looking step.
As the applicant pool grows, the number we should set for the look-and-leap rule settles to 37%. In other words, if there are 100 applicants, do not choose anyone from the first 37 applicants, after the 37th applicant, choose the first best one which is better than we saw in the first 37 applicants.
In general, if there are N applicants(items etc..), then there is chance to find best one among all of them with this formula (e is the base of the natural logarithms):
rate = N/e
Actually I do not have enough mathematical background to prove “where 37 comes from”. But there is an awesome video from Numberphile2 https://www.youtube.com/watch?v=XIOoCKO-ybQ
If we have:
-
3 numbers of applicants
-
then find the best applicant after interviewing the first one,
-
after all we have 50% change to get best one
-
-
4 numbers of applicants:
-
then find the best applicant after interviewing the first one
-
after all we have 45% change to get best one
-
-
5 numbers of applicants:
-
then find the best applicant after interviewing first and second applicants
-
after all we have 43% change to get best one
-
-
100 numbers of applicants:
-
then find the best applicant after interviewing first 37th applicants
-
after all we have 37% chance to find best one
-
As you can realize instead of choosing randomly, using look-then-leap rule we increased our chance to find the best secretary.
Before diving into the code let me to illustrate the problem with basic pictures
Example with pictures
Let’s image that we have 20 applicants
According to the our formula N/e=20/2.71=7.35 ≃ 7 , we must collect data about first 7 candidates and find the best one among them:
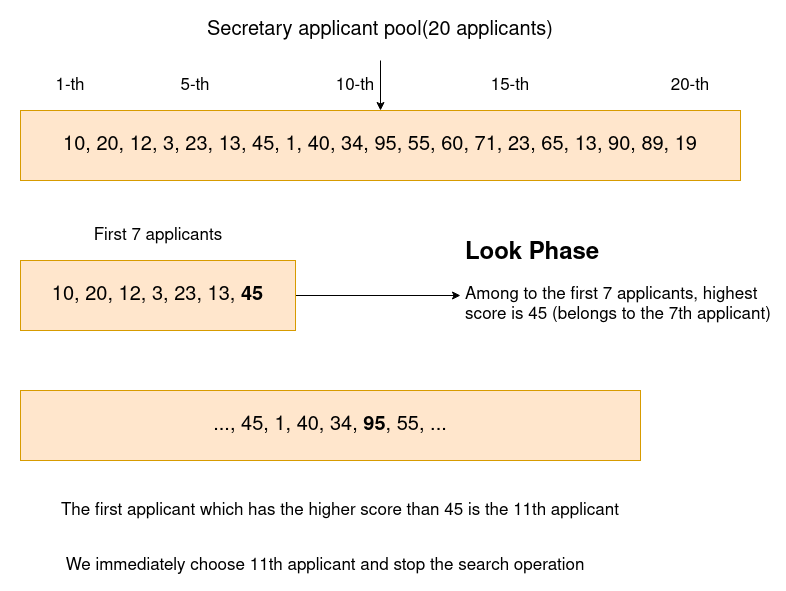
Now it is time to find the first one which is higher score than 45 (7th applicant)
As you can see 11th applicant’s score is the 95 and it is the first one after the look phase.
11th applicant has also the highest score in the applicant pool. Therefore our look-and-leap strategy succesfully worked. We have found the best secretary !!
Java Implementation
Let’s write some code about look-and-leap-rule (it will be practical implementation)
Github Link
If you only need to see the code itself, here is the link
Create basic class to represent applicants
Because we are going to simulate secretary problem, we should represent secretary as an object. Each secreatry has the following properties:
public class LookThenLeapRule {
private static class Secretary {
int score;
int index;
public Secretary(int index, int score) {
this.score = score;
this.index = index;
}
}
}
-
score: represents Secretary’s matching score to the job. Higher number means that secretary is a good candidate for our job. -
index: indicates the index of the given applicant pool(because we will store all applicants in the list, this is basically list’s index)
Generate random secretary list
Because interview with the applicants will be done in random order, we must generate random secretary list with the given size and each secretary will have score point in random manner:
public static List < Secretary > generateRandomSecretaryList(int size) {
List < Secretary > secretaryList = new ArrayList < > ();
for (int counter = 0; counter < size; counter++) {
secretaryList.add(new Secretary(counter, ThreadLocalRandom.current().nextInt(10000)));
}
return secretaryList;
}
Run look and leap rule
The rest is to about look and leap rule itself,
-
Find the best applicant among the pool. (bestInTheList)
-
Find the best applicant after the look phase (bestInTheLookPhase)
-
If bestInTheLookPhase’s score is higher than bestInTheList’s score, then our look-and-leap strategy successfully worked. I am just retuning 1 from the method to find success rate.
public class LookThenLeapRule {
// ...
public static int leapPhase(List<Secretary> secretaryList, Secretary bestSecretaryInLookPhase, Secretary bestSecretaryAmongAllApplicants, int lookPhaseCounter) {
List<Secretary> afterLookPhaseApplicants = secretaryList.subList(lookPhaseCounter , secretaryList.size());
for (Secretary secretary : afterLookPhaseApplicants) {
if (secretary.score < bestSecretaryInLookPhase.score) {
// Next applicant after the 37th applicant(index=36th, if you count from zero!!) whose score is not higher than we saw in the loop phase
// so continue with the next applicant
continue;
}
// Next applicant's score is higher than we saw in the loop phase
// We will choose the next applicant immediately because his/her score is higher than we saw in the loop phase
if (secretary.score >= bestSecretaryAmongAllApplicants.score) {
// Next applicant's score is also higher than or equal to the all applicants
// Therefore our look-then-leap strategy really worked !!
// we have found the best applicant with 37% chance
return 1;
}
break;
}
// Unfortunately, even we chose the next applicant (we are sure that her/his score is higher than in the loop phase)
// However, she/he was not the best applicant in the applicant pool.
// That's means out look-and-leap strategy failed.
return 0;
}
public static void runLookAndLeapRule(int totalApplicants, int lookPhaseCounter) {
double totalTrial = 10;
double trialUpperLimit = 1000000;
double multiplyFactor = 10;
while (totalTrial <= trialUpperLimit) {
double successfullyFound = 0;
for (int trial = 0; trial < totalTrial; trial++) {
List<Secretary> randomList = generateRandomSecretaryList(totalApplicants);
Secretary bestSecretaryAmongAllApplicants = bestSecretaryInTheList(randomList);
Secretary bestSecretaryInLookPhase = lookPhase(randomList, lookPhaseCounter);
int leapPhase = leapPhase(randomList, bestSecretaryInLookPhase, bestSecretaryAmongAllApplicants, lookPhaseCounter);
successfullyFound += leapPhase;
}
System.out.println("---------");
System.out.println("After number of '" + totalTrial + "' trials, number of '" + successfullyFound + "' times we found best applicant among all applicants(" + totalApplicants + ")");
System.out.println("Success rate to find best secretary: " + (successfullyFound*100/totalTrial));
System.out.println("");
totalTrial *= multiplyFactor;
}
}
public static void main(String[] args) {
int totalApplicants = 100; // any number except 1
int lookPhaseCounter = (int) Math.round(totalApplicants / Math.E);
System.out.println("There are " + totalApplicants + " applicants applied our job and We will look at the first: " + lookPhaseCounter + " applicants.");
System.out.println("We will find the best applicant among the first: " + lookPhaseCounter + " applicants.");
System.out.println("After the first: " + lookPhaseCounter + " applicants, We will immediately choose the one whose score is higher than from the first: " + lookPhaseCounter + " applicants.");
System.out.println();
runLookAndLeapRule(totalApplicants, lookPhaseCounter);
}
}
Run the program
Here is the output:
There are 100 applicants applied our job and We will look at the first: 37 applicants.
We will find the best applicant among the first: 37 applicants.
After the first: 37 applicants, We will immediately choose the one whose score is higher than from the first: 37 applicants.
---------
After number of '10.0' trials, number of '4.0' times we found best applicant among all applicants(100)
Success rate to find best secretary: 40.0
---------
After number of '100.0' trials, number of '42.0' times we found best applicant among all applicants(100)
Success rate to find best secretary: 42.0
---------
After number of '1000.0' trials, number of '357.0' times we found best applicant among all applicants(100)
Success rate to find best secretary: 35.7
---------
After number of '10000.0' trials, number of '3774.0' times we found best applicant among all applicants(100)
Success rate to find best secretary: 37.74
---------
After number of '100000.0' trials, number of '36992.0' times we found best applicant among all applicants(100)
Success rate to find best secretary: 36.992
---------
After number of '1000000.0' trials, number of '372248.0' times we found best applicant among all applicants(100)
Success rate to find best secretary: 37.2248
Process finished with exit code 0
As you realize, the number settles to the 37%
You can also run the program with, for example, 5 applicants. Just change the
totalApplicantsto 5. Then result will settle to the 43%
Conclusion
In this blog, we have tried to answer what optimal stopping is and we have also looked at the Look-then-Leap rule. In a sentence, we can use look-then-leap rule if we want to know “how long we should keep looking for something to find the best one”
Famous secretary problem is one of the example for the optimal stopping. And there are also many variants as well.(Such as when to sell house, when to quit etc ..)
To understand better (as a software developer), we have implemented basic program (with Java) to simulate famaous secretary problem.
Finally, if you want to get more information about optimal stopping and other famous algoritms, I strongly suggest that you read the book Algorithms To Live By.